Finite element analysis is a really cool technique that can be applied to solve lots of engineering problems. Imagine that you’re job is to model how a structural part will react when a force is applied to it. Within the material there could be trillions of atoms that are interacting with each other, some pushing and some pulling one another, how would you begin to compute those areas that are high stress? That is what finite element analysis does for us, we can break down the impossibly large problem into smaller pieces by meshing the physical structure and then computing the interactions of each node in our mesh, think of it as eating the elephant one byte at a time. 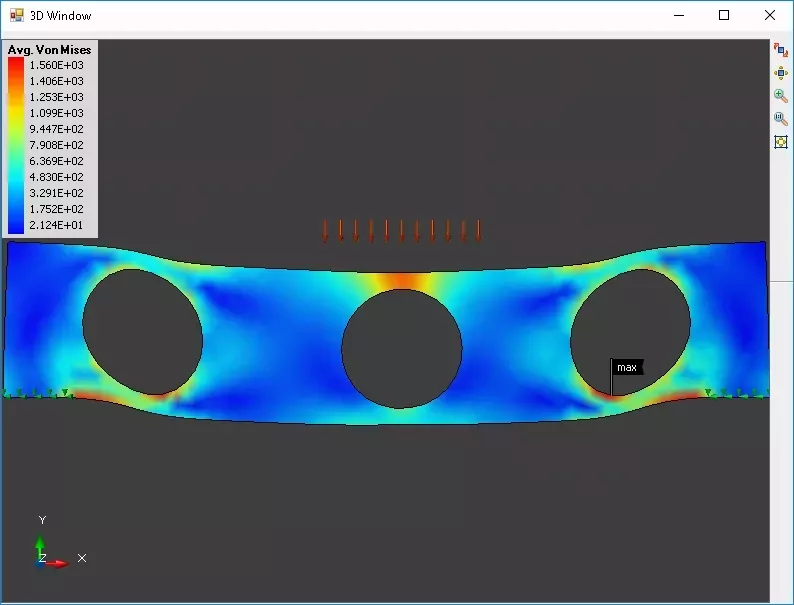
Meshing
Meshing is performed on the material structure in such a way that each of the elements is a relatively uniform size.
To setup our test we create a bar that has three large holes in it.
var mesher = new BasicMesher()
.AddLoop(new LoopBuilder()
.AddLineSegment(0, 0, 50, 0)
.AddLineSegment(50, 0, 50, 10)
.AddLineSegment(50, 10, 0, 10)
.AddLineSegment(0, 10, 0, 0)
.Build(true, 1))
.AddLoop(new LoopBuilder()
.AddArc(26, 5, 4, 0, 360)
.Build(true, 1))
.AddLoop(new LoopBuilder()
.AddArc(9, 5, 4, 0, 360)
.Build(true, 1))
.AddLoop(new LoopBuilder()
.AddArc(41, 5, 4, 0, 360)
.Build(true, 1));
Next, the mesher is invoked on the input shapes outline. After several passes of refinement a mesh of acceptable quality is produced. The result of the mesh generation looks like this 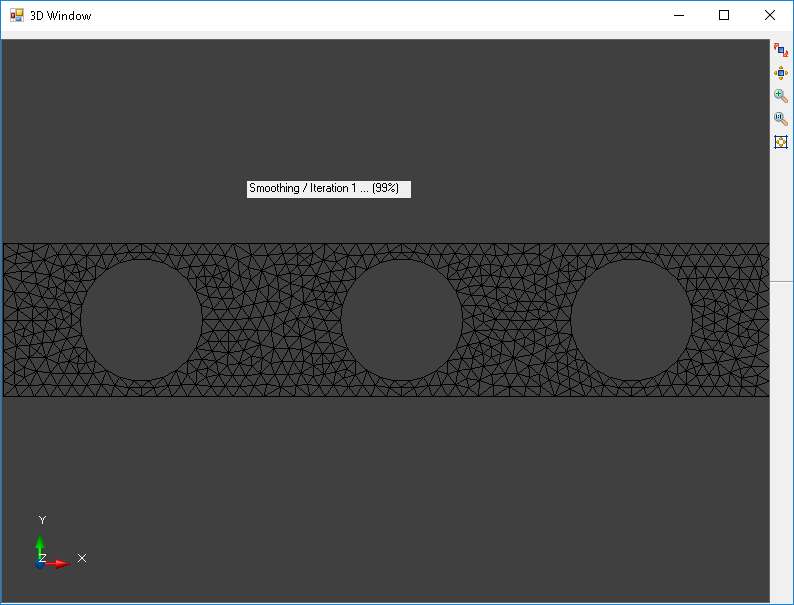
The elements within the mesh are an important consideration to producing a quality result.
Analysis
Next we assign physical properties to represent a material that our part is made of. We do this by providing values for youngs modulus and poissons ratio. Youngs modulus is the measure of a materials stiffness, that is to say it’s tendency to not deform under tensile or compressive forces. Poissons ratio describes how much a material deforms in a direction perpendicular to a tensile or compressive force applied to it, think of this as describing how much a rubber band thins when pulled.
For our test we need to put the material under some kind of stress, to do this we will lock the material along it’s bottom left and bottom right edges. This is accomplished by assigning a locking function to disallow XY movement to all nodes along these edges (the proverbial immovable object). Next we apply several large forces vectors along the upper middle boundary of the material, these vectors are facing in the downward direction (-Y) to simulate the effect of a large mass. This system is fed into the calculation engine and the effective Von Mises stress are calculated at each element in the model. We also calculated the relative displacement of all the nodes as dX and dY.
Project files are available on GitHub